Transformers for Trajectory Optimization with Application to Spacecraft Rendezvous

IEEE Aerospace Conference 2024

Tommaso Guffanti1*, Daniele Gammelli1*, Simone D'Amico1, Marco Pavone1,2,
1Stanford University, 2NVIDIA.
*Equal contribution
Paper arXiv Code Data

A Transformer-based framework to solve complex trajectory optimization problems.

Motivation

For most problems of interest, the trajectory optimization problem is usually highly non-convex, which results in formulations that are hard to solve efficiently and reliably on-board through optimization-based approaches.

At the same time, learning-based approaches for trajectory optimization, although computationally efficient, typically lack critical constraint satisfaction guarantees for reliable real-world implementation.

In this work, we propose a framework to achieve the best of both worlds:

  1. Use modern Transformer models to warm-start traditional sequential optimizers and achieve faster convergence to higher quality solutions
  2. Enforce hard constraint satisfaction within learning-based approaches through warm-starting of sequential optimizers

Our Framework

Our goal is to develop a framework to train modern Transformer models for trajectory optimization problems. Our approach can be summarized through the following steps:

Step 1: We're given an optimal control problem (OCP) defined by:

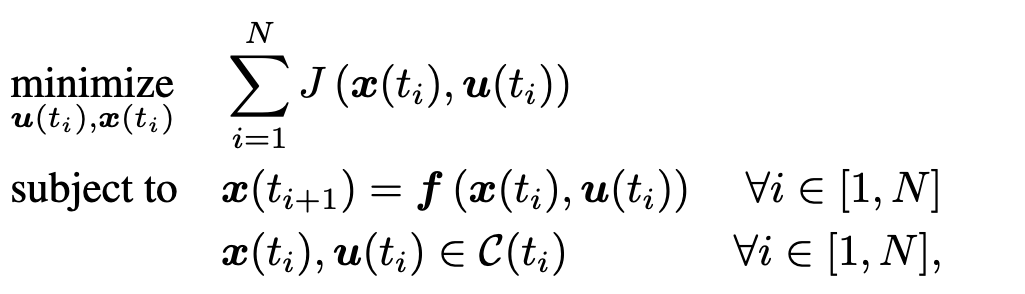
  1. Cost function J (e.g., fuel-optimality)
  2. Dynamics function f, potentially non-linear
  3. Set of constraint C(t), potentially non-convex

This setting is general and encompasses a wide variety of optimization problems of practical importance

Step 2: For the purpose of trajectory optimization, we define a trajectory as a sequence of:

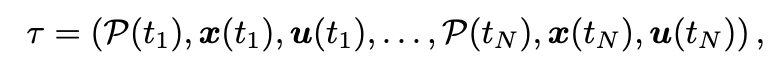
  1. Performance parameters P (more on this below)
  2. States x
  3. Controls u

Step 3: To enable Transformer training, we collect a dataset of (potentially sub-optimal) trajectories by solving the OCP in (1) from various randomized conditions

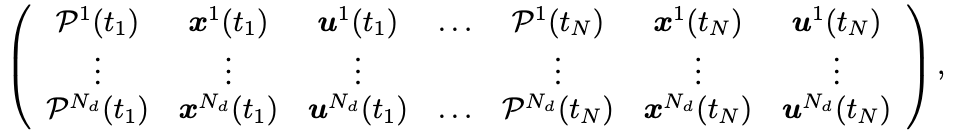
Step 4: In practice, we condition the trajectory generation using two main performance parameters:

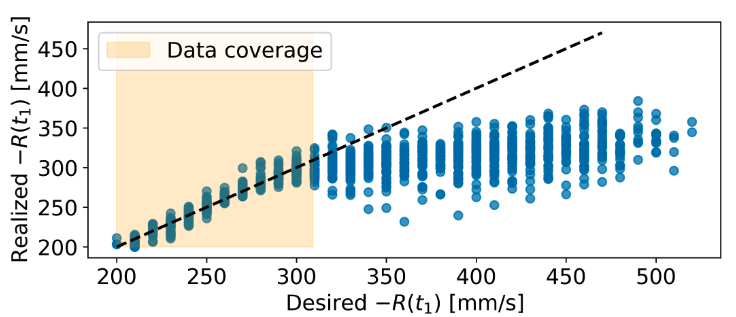
  1. Reward-to-go (R): defined as the sum of (negative) cost from time t onwards
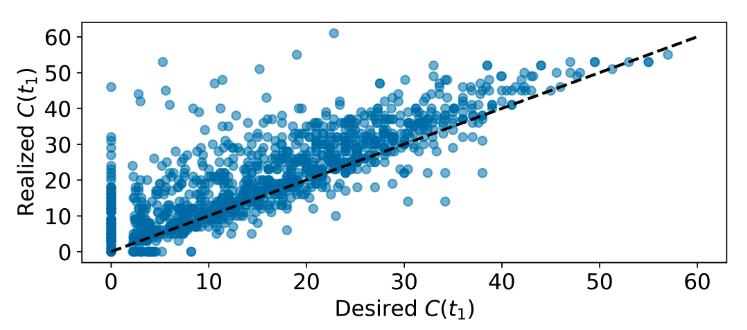
  2. Constraint-to-go (C): defined as the sum of constraint violations from time t onwards

Step 5: We train the Transformer by minimizing the squared-error loss between true and predicted states and controls

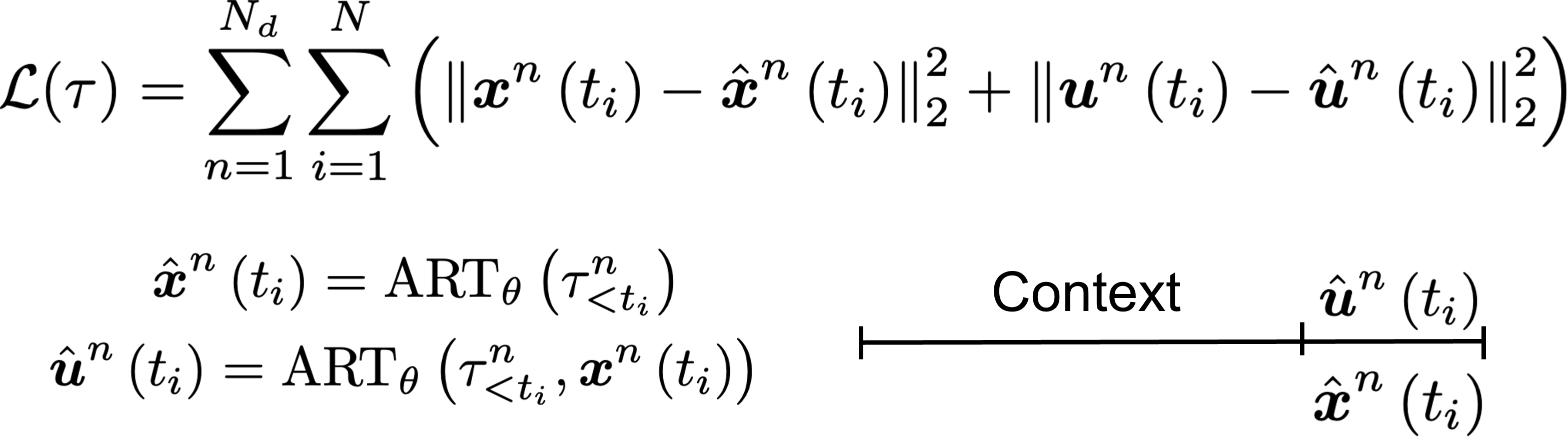
Step 6: We generate a dynamically feasible trajectory by applying transfomer-generated actions into an available dynamics model

Spacecraft Rendezvous

Warm-starting through Transformers results in convergence to higher-quality solutions, as in this docking scenario:

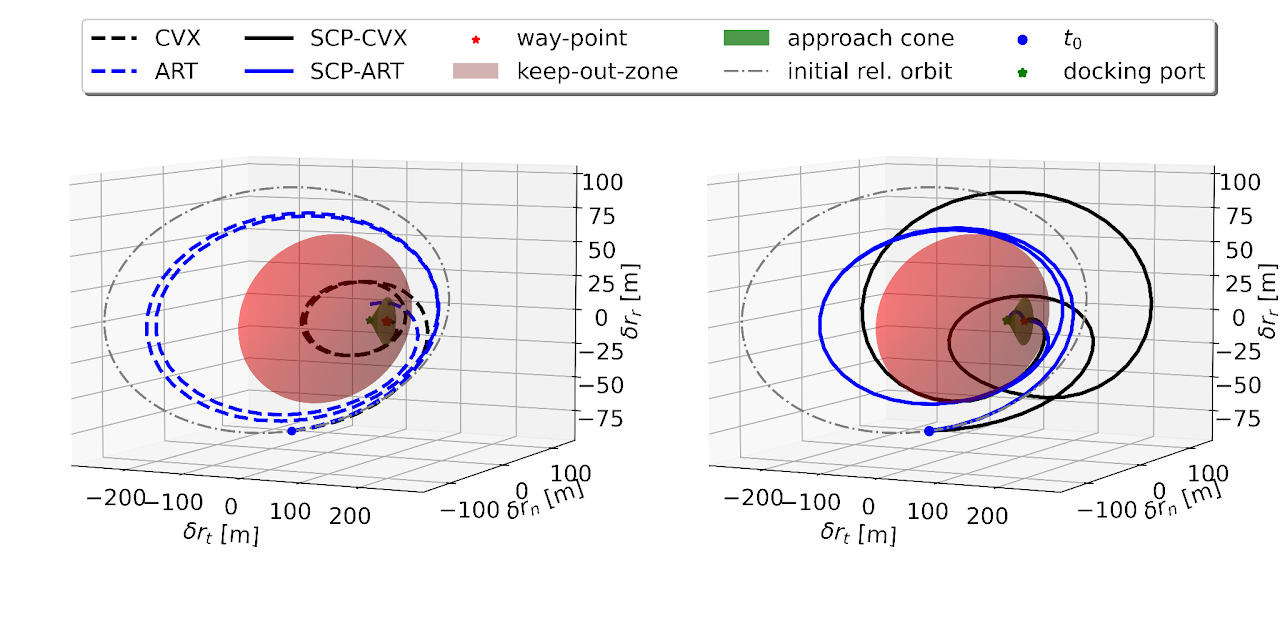
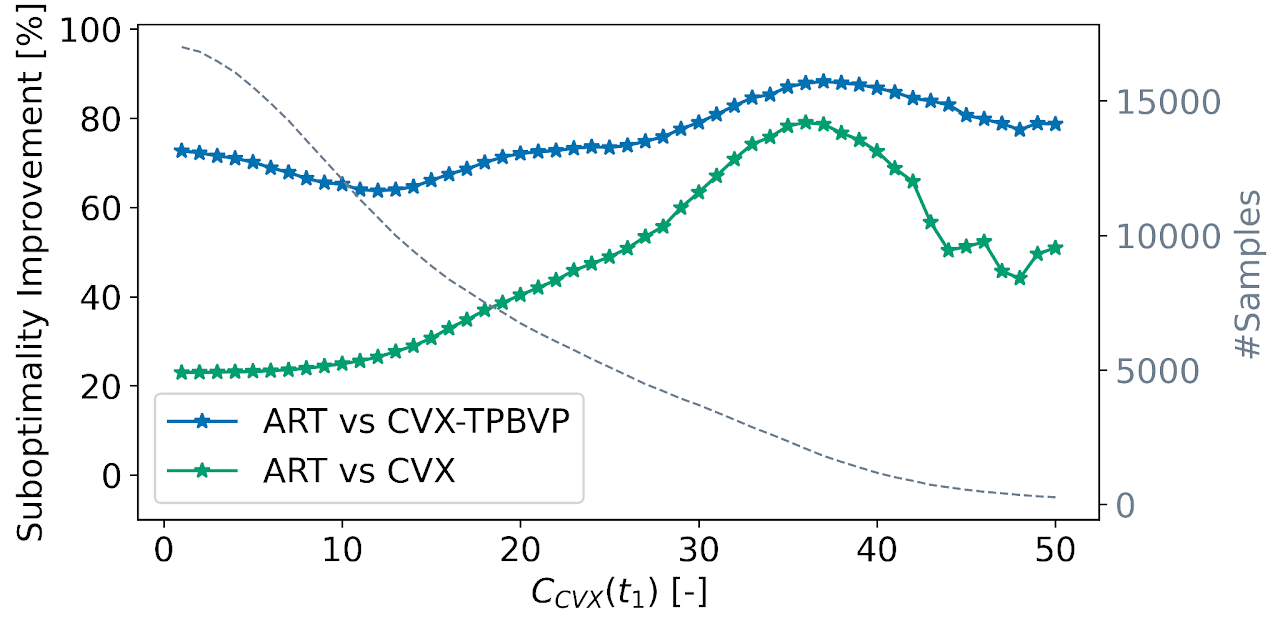
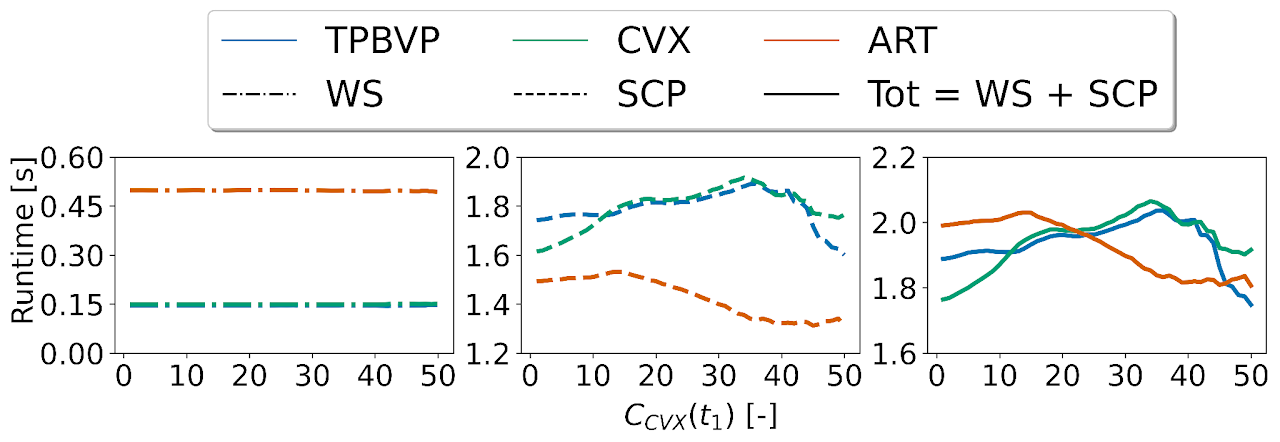
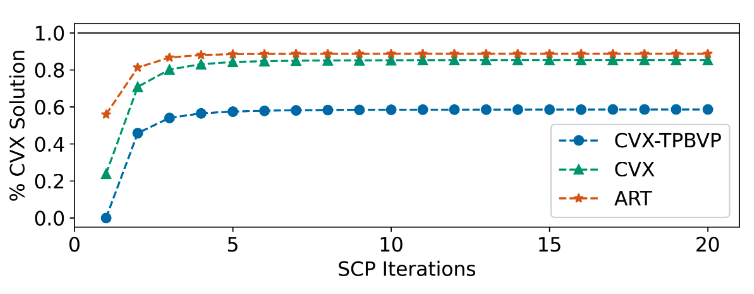
Transformers outperform competitive warm-starting methods both in terms of fuel-optimality and computational efficiency (i.e., runtime and SCP iterations)

Once trained, Transformers are able to replicate specific configurations of the performance parameter reliably, enabling a novel degree of control over the output of learning-based components

BibTeX

@article{GuffantiGammelliEtAl2024,
      title={Transformers for Trajectory Optimization with Application to Spacecraft Rendezvous},
      author={Guffanti, T. and Gammelli, D. and D'Amico, S. and Pavone, M.},
      journal={IEEE Aerospace Conference},
      year={2024}
    }